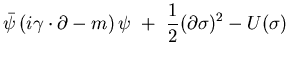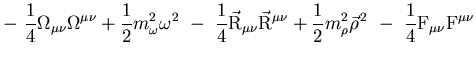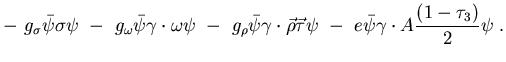

Next: Low-lying dipole strength in
Up: Collectivity of the low-lying
Previous: Introduction
Recent theoretical models based on quantum hadrodynamics
have been successfully applied in the description of various nuclear
phenomena. Mean field approximation of quantum hadrodynamics offers
accurate quantitative predictions of bulk properties from stable to the
exotic nuclei with large neutron/proton excess [6,10,9].
Collective excitations have been described within the
relativistic random phase approximation [5,3] and the
time-dependent
relativistic mean field model [7,8] in nuclei over the
whole periodic table, describing its properties that vary smoothly with
the mass number. In the present analysis we want to explore to what extent the
random phase approximation in the relativistic mean field theory can
answer the question of collectivity
in the low-lying isovector dipole excitations.
Within the relativistic mean-field theory (RMFT),
the nucleus is described as a system of Dirac nucleons interacting through the
exchange of virtual mesons and photons [6]. The Lagrangian
density reads
Here the Dirac spinor 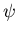 correspond to the nucleon with mass
correspond to the nucleon with mass 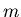 , while
, while
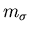 ,
, 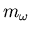 , and
, and 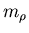 are the masses of the
are the masses of the
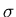 -meson, the
-meson, the 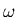 -meson, and the
-meson, and the 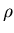 -meson.
The parameters
-meson.
The parameters 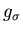 ,
, 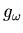 and
and 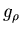 , are the coupling
constants for the mesons to the
nucleon.
, are the coupling
constants for the mesons to the
nucleon. 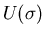 denotes the nonlinear
denotes the nonlinear 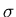 self-interaction
self-interaction
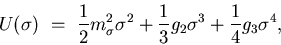 |
(2) |
and
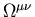 ,
,
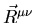 , and
, and 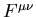 are field tensors. The non-linear
self-interaction of the
are field tensors. The non-linear
self-interaction of the  field is very important for
a quantitative description of ground and excited states in finite nuclei.
Within this model,
the Dirac-Hartree single-particle spectrum is constructed by
expanding the fields in the
harmonic oscillator basis [4] for
the spherical nuclei. The relativistic random phase approximation
(RRPA) correspond to the small amplitude limit of the time-dependent
relativistic mean field theory.
We solve the RRPA equations given in the matrix form [2];
field is very important for
a quantitative description of ground and excited states in finite nuclei.
Within this model,
the Dirac-Hartree single-particle spectrum is constructed by
expanding the fields in the
harmonic oscillator basis [4] for
the spherical nuclei. The relativistic random phase approximation
(RRPA) correspond to the small amplitude limit of the time-dependent
relativistic mean field theory.
We solve the RRPA equations given in the matrix form [2];
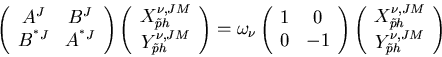 |
(3) |
where 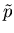 and h denotes particle(antiparticle) and hole
single-particle states within the RMFT.
The matrix elements are determined by the single-particle
energies and residual interaction,
and h denotes particle(antiparticle) and hole
single-particle states within the RMFT.
The matrix elements are determined by the single-particle
energies and residual interaction,
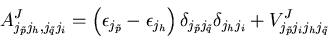 |
(4) |
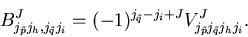 |
(5) |
Relativistic two-body interaction is obtained from the same Lagrangian (1)
with the parameter set NL3 that is used for construction
of the ground state basis [4] of single-particle energies and
corresponding wave functions.
The vacuum polarization is not taken into account,
but this effects are included
implicitly because the parameters in (1) are fitted to the experimental data
in a few finite closed shell nuclei. However, the parameters of
the interaction are fixed in further calculations and there are no additional
adjustments or special
parameters for fitting to the properties of particular excitation.
Configuration space that include only pairs
formed by excitations of particle from the Fermi sea to a higher state
above the Fermi level is not sufficient for successful description of
giant resonances. Recent investigations indicate that one should also include
the transitions from the Fermi sea to the negative-energy Dirac sea
in order to obtain decoupling of the spurious state and preserve the current
conservation [2].
Solution of the RRPA eigenvalue problem( ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) ) is applied to
evaluate the electric dipole response,
) is applied to
evaluate the electric dipole response,
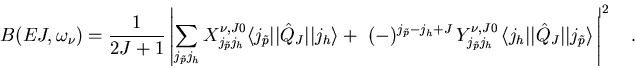 |
(6) |
For dipole excitations J=1, while 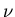 denotes the particular
RRPA-eigenvalue.
The presence of the spurious state corresponding to the center of mass
motion, should be carefully treated. In the case of ideal accuracy, the
spurious state is degenerate with the ground state, while because of the
truncation effect, one can expect low energy spurious peak. A large
dimension of the configuration space is suggested to ensure that the
spurious component is eliminated from the physical states [2].
To avoid the coupling of the spurious state to electric transition operator,
the following isovector dipole operator is applied,
denotes the particular
RRPA-eigenvalue.
The presence of the spurious state corresponding to the center of mass
motion, should be carefully treated. In the case of ideal accuracy, the
spurious state is degenerate with the ground state, while because of the
truncation effect, one can expect low energy spurious peak. A large
dimension of the configuration space is suggested to ensure that the
spurious component is eliminated from the physical states [2].
To avoid the coupling of the spurious state to electric transition operator,
the following isovector dipole operator is applied,
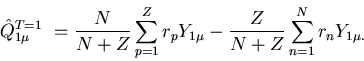 |
(7) |
When considering isovector dipole modes, the contributions from Dirac
states do not contribute significantly, in contrast to the large
effect to the RRPA strength distributions in the isoscalar case,
where contribution
of scalar 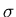 -meson dominates if compared with the role of the
vector
-meson dominates if compared with the role of the
vector 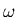 and
and 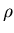 -mesons [28].
The isovector dipole strength distribution
for the
-mesons [28].
The isovector dipole strength distribution
for the 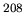 Pb is shown in the Fig.1, separately for
calculations without and with Dirac states contributions due to
exchange of scalar and vector mesons. The exact position of
GDR energy is independent from the contributions of antiparticle-particle
excitations, but without it, only 2/3 of dipole strength in the main
peak is exhausted. Therefore in the further analysis, we apply the full
self-consistent RRPA including in addition to the ordinary p-h excitations,
the antiparticle-hole excitations from the occupied Fermi to
the empty Dirac sea.
Pb is shown in the Fig.1, separately for
calculations without and with Dirac states contributions due to
exchange of scalar and vector mesons. The exact position of
GDR energy is independent from the contributions of antiparticle-particle
excitations, but without it, only 2/3 of dipole strength in the main
peak is exhausted. Therefore in the further analysis, we apply the full
self-consistent RRPA including in addition to the ordinary p-h excitations,
the antiparticle-hole excitations from the occupied Fermi to
the empty Dirac sea.


Next: Low-lying dipole strength in
Up: Collectivity of the low-lying
Previous: Introduction
Nils Paar, 2001.